Dropping ladders

My friend Rhett Allain has really got me interested in this ladder drop posted by Veritasium:

Here’s Rhett’s awesome explanation:

Of course I wanted to see if I could model it with Mathematica, and, after finding I could run Mathematica for free on my windows laptop, I thought I’d revisit this problem, since I think I found something interesting.

Physics involved

Here’s what I did:

• I modeled the rungs of the ladder as rigid sticks with a mass, a length, and moment of inertia
• I modeled the ground as a one-way spring (it only pushes up if either end of the rung goes below the ground, it doesn’t pull back down when either end is above the ground)
• I modeled the strings holding the rungs together as one-way spring as well. If they stretch, they pull. If they’re compressed, they do nothing.
• I modeled frictional energy loss by treating the ground as a viscous fluid. Any time either end is under the ground, there’s a frictional force proportional to the speed of that end that is in the opposite direction of the motion. Here’s a youtube vid I made about that approach.

I did all of that in a Lagrangian formalism. The one-way springs are piecewise potential energy functions, for example.

I had to play around with the strength of the ground one-way spring to make sure the bounces seemed realistic and also with the amount of viscous friction so that the rungs came to a stop relatively quickly.

What it looks like

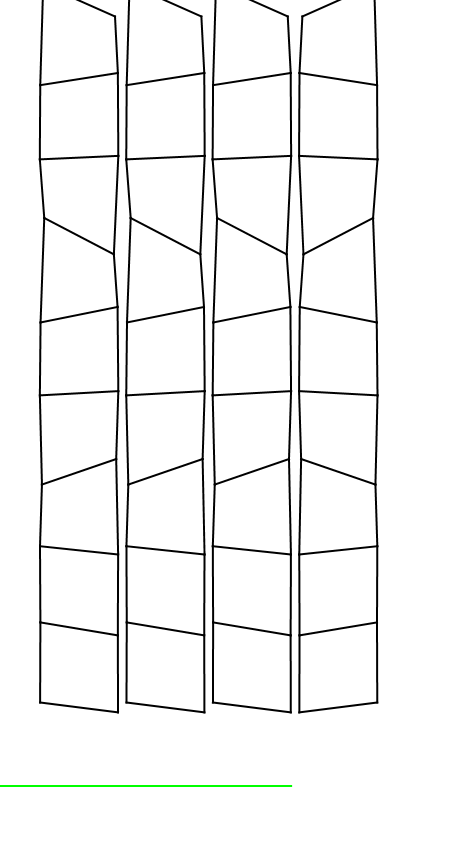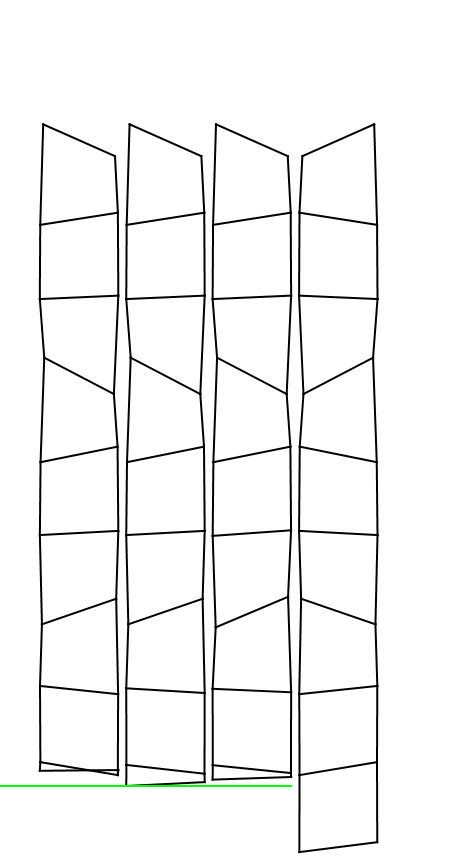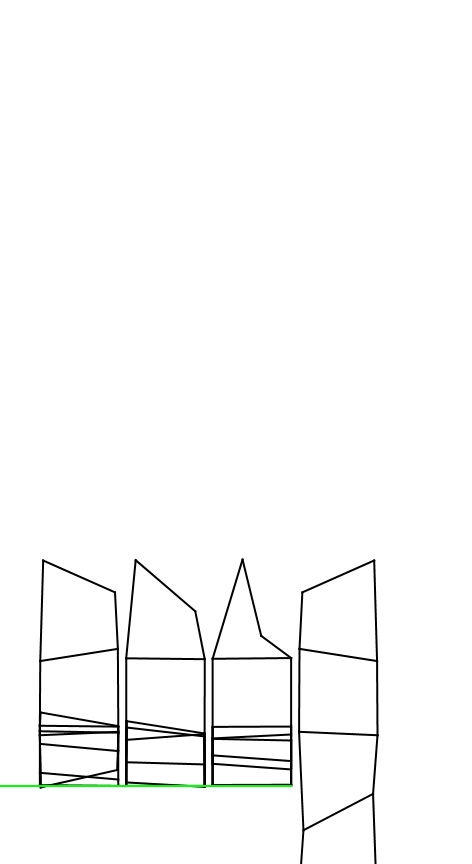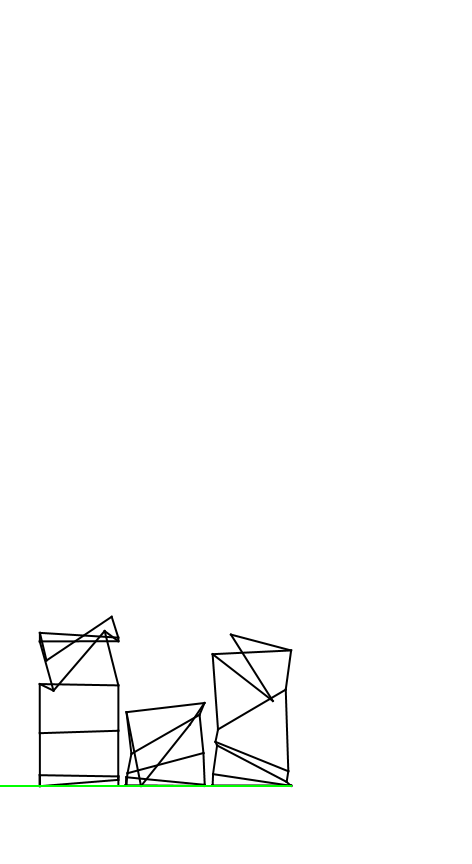
Here’s an animated gif showing 4 very similar ladders. From left to right:

• Moment of inertia of each rung is
• Moment of inertia of each rung is
• Moment of inertia of each rung is
• Free fall (doesn’t hit the ground so the moment of inertia doesn’t matter)

Here’s a plot (along with a zoomed-in inset) of the height of the middle of the top rung for each of those ladders:

You can see that the smaller the moment of inertia of the rung, the faster it falls.

Using Rhett’s explanation (which I really think is right), when a tilted (that’s important!) rung hits the ground, it slaps down the other end, which stretches the string tied to that end, which then pulls down, at least slightly, on the rung above it. This continues in a domino like fashion. Ultimately all that “pulling down” is what accelerates the top rung faster than free-fall.

The differences for the moment of inertia is what I find interesting. The one is a rung that has a uniform cross-section (ie, the mass is uniformly spread through the length). The one is what you get if all the mass of the rung is at the ends. Really this is the highest possible moment of inertia for a rung. The lowest possible is zero if all the mass is in a point mass at the center, but for fun I did to see a more obvious effect. With a higher moment of inertia, the “slaps down” effect I talk about above is lessened, because the rung is harder to rotate. That means the “pulls down” effect is lessened as well and so you see that there’s less additional acceleration for the top rung. In the plot above you can see that the maximum moment of inertia is indistinguishable from free-fall.

Your thoughts

I’d love to hear what you think. Here’s some starters for you:

• I love this! I’m going to build a minimal moment of inertia ladder right now.
• This is dumb. What you totally missed in your model was . . .
• I don’t know why you insist on using such an expensive tool like Mathematica . . . wait, what did you say in your last post?
• I don’t like your friction model. Instead I think you should . . .
• I think your rungs are bouncing too high, you should raise your friction amount. (I did that but found that it reduces the “slap down” too as it doesn’t just cause rotation, it also moves the end a little bit. Something to think about, I guess)
• I think all ladder rungs are uniform. This is stupid.
• I think Veritasium doctored that first video. There’s no way there’s two ladders with every rung angle being exactly the same.
• Hang on a sec, it looks like you’ve pinned the center of the rungs on a vertical line. That’s crap and you know it.
• Are you saying that if all the rungs are perfectly horizontal nothing happens? How boring.