Relativistic explosions

Earlier this week I got an email from a friend who has been working with his students modeling how momentum works in a situation where two carts start connected and then explode apart. I’m not sure, but I think that he might be using something like the spring-loaded Pasco carts. You connect them, set the spring, and then press the release. He then has his students measure the final speeds of the carts. He has them change the relative mass of the carts in an effort to see what the commonalities are.

He suggests that they plot the velocity ratio $v_2/v_1$ versus the mass ratio $m_1/m_2$ (note the change in indices). I think this is a very cool way to approach this lab. If things work the way we expect them to, that graph should be linear, with a slope of 1.

What my friend asked was what would happen as the speeds got to a relativistic regime ( $v_i\lesssim c$ ). He wanted to let his students know that if they could take more data, eventually the points would not fall on the line. What he asked me about was which way it would miss.

I realized that it’s a complex question. Relativistic momentum ( $p=mv/\sqrt{1-v^2}$ ) has that nasty radical in it, making the analysis difficult. So, as usual, I opened up Mathematica to play around. The first thing I tried was to solve the energy and momentum equations in 1D for this explosion process:

$(m_1+m_2)c^2+E_\text{explosion}=\frac{m_1 c^2}{\sqrt{1-\frac{v_1^2}{c^2}}}+\frac{m_2 c^2}{\sqrt{1-\frac{v_2^2}{c^2}}}$

$\frac{m_1 v_1}{\sqrt{1-\frac{v_1^2}{c^2}}}=\frac{m_2 v_2}{\sqrt{1-\frac{v_2^2}{c^2}}}$

However, Mathematica failed (or at least ran until I got tired of waiting). I had a suspicion that it would do better if I put in a few numbers (like the masses and energy) and, sure enough, it’s able to figure out the velocity ratio when I do that. I’m still not quite sure why it fails with generic algebraic values for the masses and energy, so if you have some good ideas, pass them along!

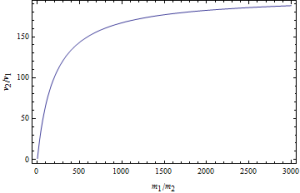
But, doing it numerically was still useful. Here’s a plot of the velocity ratios vs the mass ratios for an energy that’s a few orders of magnitude less than the mass energies of the particles:

velocity ratio to mass ratio for a low energy explosion. The pink link is the classical expectation

You can see that as the mass ratio gets large, the expected velocity ratio is less than what is expected classically. Here’s another with a much larger energy:

velocity ratio vs mass ratio for larger energy

Here we see that it deviates quite a bit from the classical expectation.

When I showed this to my friend, he thought it was interesting that it looks like it’s approaching an asymptote, musing that it must have something to do with the universal speed limit (nothing can go faster than c, so that must affect the limits of the speed ratio of this experiment).

So I began playing around some more, and I found that it goes towards an asymptote no matter what the energy is (though for some really low energies, you have to go out to huge mass ratios to see it). I wondered if I could predict where that asymptote would be, and I got half-way there. For low energies, I can do it, but for high energies, I’m stuck and would love some help.

So first the low energies. Note that doing all of this in $\LaTeX$ is fine, but I wanted to show off the handwriting capability of my new Microsoft Surface Pro 2:

derivation of the low energy asymptote

I assume that for any energy ( $\alpha m_1 c^2$ ) you can find a mass ratio large enough that $\alpha m_1/m_2$ is much larger than 1. That jives with the notion that for low energies I have to go way out on the mass ratio axis to see the asymptote:

velocity ratio vs mass ratio for low energy with alpha=0.005

Note how it is approaching an asymptote at v2/v1=200 as expected for $\alpha = 0.005$ .

Unfortunately, I’ve really struggled trying to do the same thing with larger energies. Certainly I can make plots of it, but I’m unable to find an analytic expression. Please help if you can.

One last thing. I was curious what would happen at very large energies (larger than the mass energies of the surviving particles). What I found was a velocity ratio that tended to one (just a little larger than one, of course). At first I was confused, but then I realized that if the particles have to carry away a lot of energy, even the heavy one likely has to get moving, and if they’re both moving quite fast, they’re both running up against the speed limit. Very cool.

So, can you help me out? Here’s some starters for you?

I’m confused, why do you care about this?
I don’t like the assumptions you’re making in your low energy derivation, I’d prefer to see it done . . .
I know exactly how to do the high energy case, it’s trivial!
Why don’t you use awesome interactive graphs like Rhett Allain does?
I would have read this post, but you mentioned Mathematica and I stopped.
How do you like your Surface Pro? Blog post in the future?
I much prefer LaTeX to handwriting, please don’t ever do that again.
I know why Mathematica choked on the generic solve. All you have to do is . . .

2 Responses to Relativistic explosions

Andy "SuperFly" Rundquist says:

April 6, 2014 at 1:48 pm

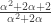
I wanted to get this down before I forgot about it. I found a way to get Mathematica to do this analytically. The result is that the asymptote as a function of $\alpha$ is $\frac{\alpha ^2+2 \alpha +2}{\alpha ^2+2 \alpha }$

Andy "SuperFly" Rundquist says:

November 19, 2014 at 11:09 am

My friend Leon Webster has a geometric way to think about this. Here’s a link to his notes (pdf) https://drive.google.com/file/d/0B-N21MFujA8BX05LamlaSzVOcXp3dnUzaEhmakgtVzNLY0ZV/view?usp=sharing