Situations that share equations of motion

Recently my friend Rhett Allain has been making some awesome videos showing how to solve complex problems with a Lagrangian approach. I love it when he posts a new video because it usually motivates me to try to model something similar.

Here’s the video he posted that inspired this post:

Rhett’s vid about two masses tied together through a hole in a table

I love this particular problem so I decided to dig in and see what I could learn from building my own model of it. One thing I was curious about was whether using a Lagrange multiplier technique could save me time. Basically I wondered if I could just model the two balls quite simply using Cartesian coordinates (xyz coordinates) and then directly imposing a constraint on the length of the string between them.

Unfortunately my first attempt had a huge mistake in it leading me to make an erroneous claim in this response video:

My initial video response to Rhett that has a big mistake in it (can you spot it?)

I got so excited that I had found an analogous system that shared the equations of motion, only upon reflection I realized I’d made a big mistake.

The length of the string should be given by the length above the hole:

along with the length of the string below the hole:

My mistake was assuming that was equivalent to:

Do you see the mistake? I hope it takes you more than a second or two to see it because I spent half a day thinking I’d discovered something really cool! Note that I still wrote this post so, trust me, there is still something cool, just not what I thought it was!

So what was I thinking? Well, let’s look at the code:

First let’s assume the masses are the same. Then the kinetic energy (the line starting with “T=”) would just be the kinetic energy of a free particle. In other words this would be just the model of a ball flying through a simple gravitational field. But that then gets corrected with the constraint line (the one that starts “cons = “). That says that the sum of squares of the variables needs to be a constant. That would imply that the particle has to stay on (or inside of) the surface of a sphere.

That’s what I got excited about in my video, because it seemed like the problem of the two balls connected through a hole with string was identical in form to a ball that has to stay on a sphere in a gravitational field. In hindsight I realize that a better way to describe that latter analogous problem is to call it what it is: a 3D pendulum!

But, ugh, I got the constraint wrong. It should have been that the length of string (which is held constant) is given by:

Of course in my case I put the hole at z=0 with “up” representing positive z’s. In other words the z in this problem will always be negative. So that gives:

Making that correction to the “cons = ” line gives me the correct model of the two particles tied together by a string running through that hole.

Now, here’s the cool part. If you set the masses equal, you can interpret the kinetic and potential energies (along with the constraint) to be describing a system where a ball has to stay on a surface described by that constraint.

Here’s what that looks like side by side:

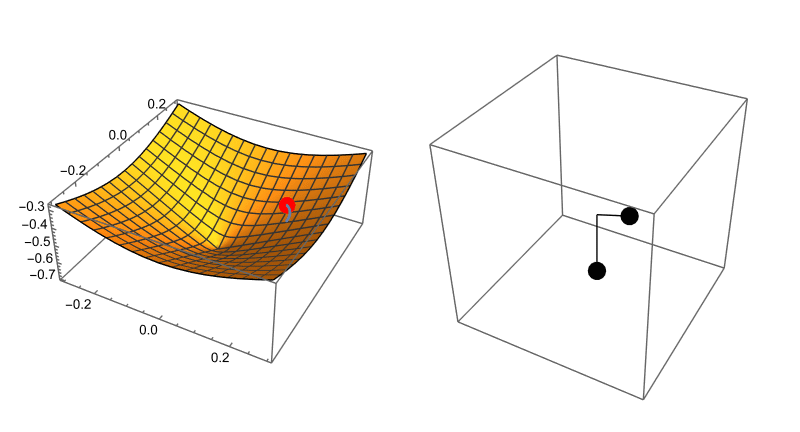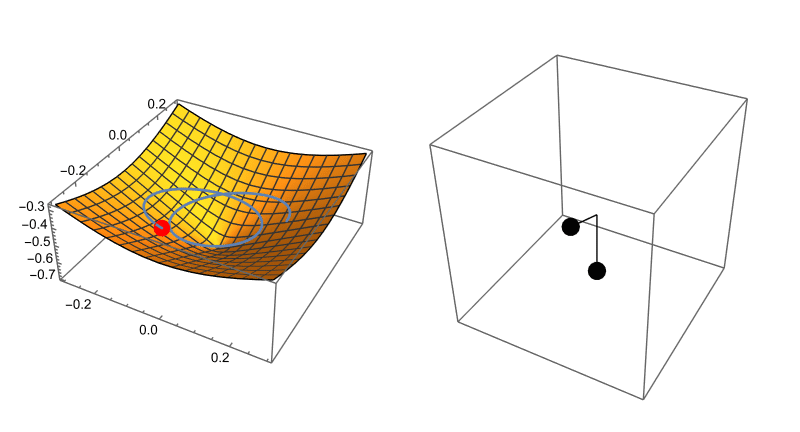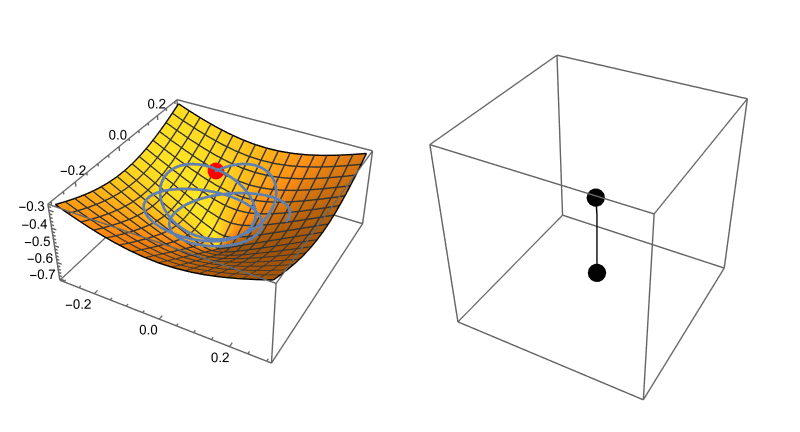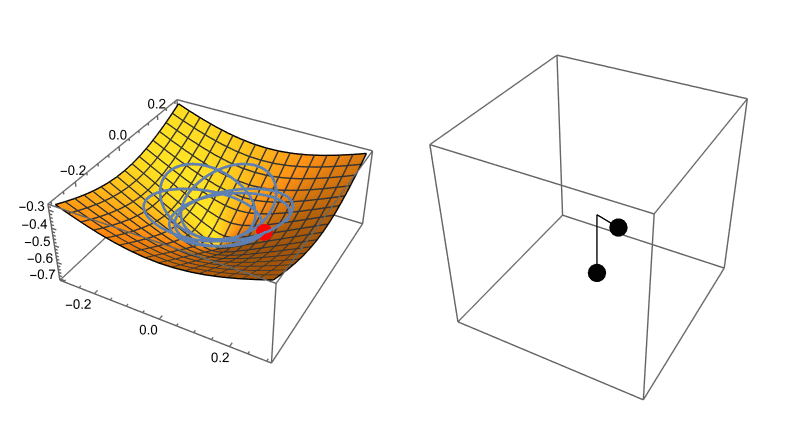
See. I told you. Cool!

Your thoughts?

So what do you think? Here are some starters for you:

1. This IS cool. What I especially liked was . . .
2. Um, this isn’t cool, thanks for wasting my time. What I especially disapprove of is . . .
3. Let me get this straight: in an effort to look smart you posted a youtube vid that has a huge error in it and still thought you might as well post that mistake-ridden vid in this post. Loser.
4. This is Rhett. You’re awesome.
5. This is Rhett. Stop stalking me.
6. Why do you use the Lagrange multiplier approach? Are you afraid to type sines and cosines or something?
7. Lots of systems share a set of equations of motion. Why do you think it’s cool?
8. It took me exactly 2.3 seconds to find your dumb mistake.